Estos tipos de estructuras están constituidos en su mayor parte por piedras ligadas con hormigón o cal o también con hormigón simple. Su aplicación resulta ventajosa en aquellos sitios montañosos en los que se dispone de buena piedra, como son las que proceden de rocas eruptivas y que no están en descomposición.
Estos puentes son construidos en forma de bóveda utilizando la mampostería de aparejos especiales, lo que requiere de un estudio prolijo de los cortes de las piedras, en la actualidad resulta mejor ligar las piedras con mortero de cal o mejor con hormigón que permite obtener acabados similares a los de mampostería de aparejos utilizando piedras talladas en la parte vista y que no intervienen como elementos resistentes.
|
Con este tipo de bóvedas se puede alcanzar en forma económica hasta 15 metros, no siendo aconsejable luces mayores debido al incremento enorme de su peso propio.
En la actualidad no se construyen bóvedas mayores, a los 8 m. de luz porque existen formas más económicas de solución.
En el pasado se ha utilizado mucho este tipo de construcción debido a que en general los trazados camineros se los realizaba por regiones cordilleranas a las que el transporte de otros materiales resultaba difícil, es por esta razón que se pueden observar muchos puentes pequeños y alcantarillas de piedra. Estos materiales tienen la ventaja de ser baratos en lo que a mantenimiento respecta y por otra parte, su aspecto es satisfactorio, presentando una gran rigidez frente a otros tipos de estructuras mas esbeltas.
En algunos casos se construyen estos puentes sin piedras, es decir en hormigón simple, resultando estructuras mas caras, debido a la utilización de encofrados especiales y mayor consumo de cemento, por lo que en esos casos resulta mas adecuado recurrir al hormigón armado.
Tipos de bóvedas simples de mampostería.
La forma clásica de distinguir las bóvedas es por la relación de su flecha f a su luz L, de modo que cuando la relación f / L < 1/2 la bóveda es rebajada y cuando f / L>1/2 se tiene la bóveda aperaltada, el caso intermedio cuando f / L = 1/2 se denomina arco de medio punto.
Partes constitutivas de una bóveda.
Se pueden distinguir los siguientes elementos:
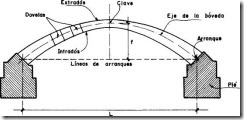
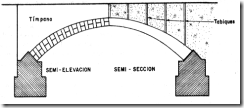
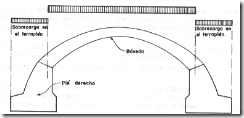
La bóveda propiamente dicha que corresponde a la superestructura y los pies derechos a la infraestructura y que son los que absorben y transmiten los empujes del arco ver figura.
|
El eje de las bóvedas puede ser: Una parábola, una elipse, un arco de círculo, un arco de varios centros o mejor aún la curva funicular de las cargas que actúan sobre el arco.
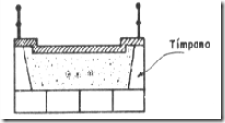
En corte transversal, ver figura la bóveda puede llevar muros laterales denominados tímpanos que son muros de contención del relleno de tierra que se coloca en medio de ellos hasta alcanzar el nivel de la calzada.
|
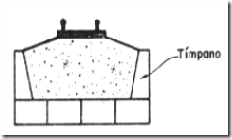
Cuando el relleno es muy alto y la calzada estrecha es conveniente ligar estos tímpanos por medio de muros o tabiques transversales. Caso en el que tanto los muros como los tabiques se los construye en hormigón armado, ver figura.
|
En las bóvedas para puentes ferroviarios, las durmientes pueden ir directamente sobre el relleno si este es de grava o arena, porque si es de tierra, se deberá colocar una capa de ripio o balasto para recibir los durmientes.
El extradós de las bóvedas debe ir impermeabilizado antes de colocar el relleno para así evitar que las filtraciones manchen el intradós y ocasionalmente provoquen daños a la estructura. El espesor mínimo del relleno en la clave debe ser de 0.3 m.
Cálculo de las bóvedas en mampostería
Las bóvedas de mampostería se emplean en pequeños desagües o alcantarillas, por ello es que dada su reducida luz se las puede calcular como Inarticuladas (en la clave y los arranques) y se las construye sin estas articulaciones.
En el cálculo habrá que considerar:
a) El peso propio de la bóveda.
b) El peso del relleno.
c) La carga viva uniformemente repartida.
d) Empuje de tierra en los estribos.
Este último tiene importancia porque la reacción será máxima si se coloca la sobrecarga en la bóveda y no en el terraplén de acceso y al contrario, se obtendrá el máximo empuje cuando la bóveda está descargada y el terraplén cargado.
Con estas dos hipótesis se llega a tener dos líneas de empujes diferentes que pueden ser consideradas como las líneas límite dentro de las que se van a situar las líneas de carga para las etapas intermedias.
|
En base a la estática gráfica es posible resolver el problema para lo que se deben conocer además de las cargas exteriores, tres puntos de paso del polígono, una de las reacciones oblicuas en posición y magnitud, o la posición de las dos reacciones aunque sus valores no sean conocidos.
Habiendo sido trazado el polígono se pueden determinar las solicitaciones en una sección cualquiera de la bóveda, como ser el esfuerzo cortante V, el normal N y el momento flexor M.
En el caso de las bóvedas se hace pasar el polígono por tres puntos, ubicados dos en los arranques y uno en la clave.
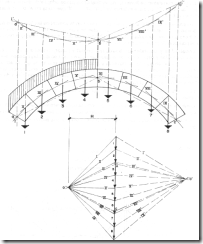
Sea una bóveda cargada en su mitad izquierda con una carga uniformemente distribuida según se muestra en la figura y con el peso propio descompuesto en dovelas sobre las que también se adiciona por partes la carga distribuida con lo que se obtienen los pesos 1, 2, 3, y 4 y por las dovelas de la derecha los pesos 5, 6, 7 y 8.
|
Las paralelas O'A, O'C a b'a' y b'c' determinan en la vertical de las fuerzas los puntos A y C por los que se trazan otras dos paralelas a las rectas ba y be, quedando fijado un nuevo polo O, con el que se traza un nuevo funicular I, II, III, ........X partiendo de a. Este funicular que deberá pasar por b y c es el polígono de presiones de la bóveda.
Encofrados y puntales de bóvedas.
Se debe poner particular atención en el hecho de que los encofrados y especialmente los puntales para este tipo de obras deben ser robustos e indeformables porque en general las bóvedas y arcos losa tienen una forma que se adapta a la línea de presiones, lo que significa que si se produce una deformación en los encofrados, la bóveda o el arco cambiaría de forma traduciéndose esto en tensiones tanto de tracción como de compresión que no han sido previstas en el cálculo.
El apuntalamiento o cimbrado puede ser clasificado de la siguiente manera; Sistemas cerrado, abierto y mixto.
Cimbras cerradas.
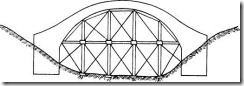
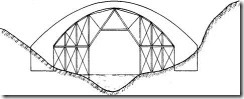
Son aquellas que tienen apoyos intermedios a lo largo de todo el arco ver figura y se las aplica cuando el río tiene poco caudal o se seca en época de estiaje.
En forma relativamente aproximada se pueden estimar sus asentamientos con la siguiente expresión:
Donde:
L = Luz de la bóveda.
f = Flecha de la bóveda.
= Asentamiento esperado.
|
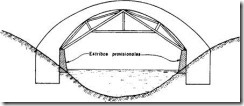
Son aquellas que no llevan apoyos intermedios y transmiten toda su carga por dos puntos de apoyo extremo ,ver figura, debido a que se trata de obras de arte construidas sobre ríos caudalosos aún en época de estiaje o sobre vías en las que no se puede interrumpir la circulación inferior.
|
Los puntales o cimbras de un arco normalmente son ejecutados con una parte fija y otra móvil. La parte fija la constituye el reticular de la zona inferior y sobre ella se colocan los aparatos de desapuntalado y en la parte superior se tiene la zona móvil sobre la que se apoyan los encofrados permitiendo que en el momento del desencofrado entre de inmediato en tensión el arco.
En las cimbras abiertas, la parte fija se la construye junto a los apoyos del puente, inclusive en algunos casos, se aprovechan los mismos estribos para que trabajen como parte fija. Otras veces, los puntales están constituidos por reticulares separados entre 1 y 1.5 m. y que transmiten las cargas de las bóvedas a los apoyos a condición de no admitir grandes deformaciones.
Los apoyos de los pies derechos sobre el terreno deben ser puntos de apoyo efectivo para que la masa no sufra asentamientos, por ello es que si el terreno superficial es firme y sin peligro de socavación, se puede emplear simples durmientes de madera o enterrando los pies derechos a manera de pilotes, pero si el terreno no es firme habrá que vaciar en el lecho del río dados de hormigón o de mampostería para recién sobre ellos apoyar los puntales. Otra solución en estos casos consiste también en hincar pilotes, ya sean de acero o de madera.
Cimbras mixtas.-
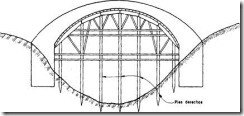
Son aquellas comprendidas entre los dos sistemas anteriores y que tienen diversidad de soluciones como ser las que se muestran en las figuras.
En las cimbras mixtas el asentamiento que se puede esperar está dado por:
Preferentemente los puntales deberán ser metálicos, sin embargo por razones de economía pueden ser de madera, en ambos casos deben ser controlados en cuanto a sus deformaciones se refiere. El uso de puntales metálicos se justifica cuando se va a construir varias bóvedas.
|
En su forma definitiva los encofrados deben llevar un peralte o contraflecha para compensar el asentamiento y la flecha que se producirá cuando gravite sobre ellos el material constitutivo de la bóveda.
|
Para prever esta contraflecha es aconsejable recurrir al empirismo, midiendo los asentamientos de los andamies cuando se los somete a carga experimental conocida y extrapolando valores para la carga real que soportarán los mismos. Para las cimbras cerradas y para las mixtas, se pueden aplicar las anteriores expresiones.
Desencofrado de arcos.
En función de la magnitud de la obra se debe prever los aparatos de desencofrado para que esta operación sea lenta y uniforme. El desencofrado se lo debe realizar bajo la vigilancia de un ingeniero o un técnico entendido en la materia.
El descimbrado lento es para evitar que la bóveda se ponga en tensión bruscamente porque luego del desencofrado la bóveda entra a trabajar en algunos casos con sus fatigas máximas admisibles.
El descimbrado debe ser uniforme porque si se quitan los apoyos en forma irregular puede suceder que algunos puntos tomen la carga de la cual han sido liberados otros, resultando que si esta carga es excesiva provocará la ruptura del andamiaje y en consecuencia el descimbrado prematuro que puede también provocar el colapso de la estructura.
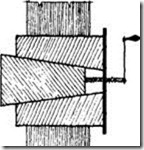
Para la operación del desencofrado lento y uniforme existen diferentes aparatos diseñados según la importancia de la obra, así cuando se trata de obras pequeñas será suficiente el sistema de cuñas, una de ellas fija y la otra móvil, ver figura 5.37 a , formando un pequeño ángulo con relación a la horizontal. Esto siempre que la carga sea reducida porque de lo contrario puede ocurrir que una de las cuñas se incruste en la otra, con la consecuencia de una dificultosa operación de desencofrado y con el riesgo de no cumplir con su objetivo.
Es mejor colocar tres cuñas forradas con calamina de modo que mediante un tomillo se puede accionar la cuña central, ver figura b.
|
|
|
Figura Diversos aparatos para el descimbrado.
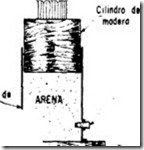
En obras de mayor importancia se utilizarán los llamados cajones de arena, ver figura c, que están constituidos por un cilindro metálico con su parte inferior cerrada con una tabla, apoyándose directamente sobre el terreno o la base que haya sido prevista para darle un apoyo adecuado. En su parte superior el cilindro recibe un pistón de madera dura que transmite la carga de los puntales a un relleno de arena fina, grano uniforme y exento de arcillas. El cilindro lleva en su parte inferior un tapón de madera que para la operación de descimbrado se lo saca y la arena va fluyendo lentamente por él y para que el desencofrado sea uniforme se deben extraer simultáneamente los tapones de todos los aparatos instalados.
Estos aparatos son económicos y tienen además la ventaja de su fácil manejo porque inclusive si se desea parar la operación es suficiente volver a colocar el tapón, esto puede ser necesario cuando por alguna razón como ser formación de grumos, se obstruye el hueco de salida.
Finalmente, todos estos sistemas pueden ser ventajosamente reemplazados con gatos hidráulicos que permiten un perfecto calibrado.
Fórmulas para el dimensionamiento.
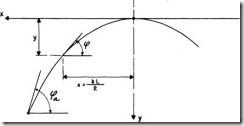
Tomando como ejes de referencia los de la figura, se tiene:
El eje del arco está dado por una de las dos expresiones siguientes:
Las tangentes de estas ecuaciones son respectivamente:
En estas expresiones:
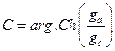= Argumento coseno hiperbólico
Donde:
ga = Carga muerta sobre el arranque.
gc = Carga muerta sobre la clave.
x = Distancia variable medida desde la clave.
L = Luz del arco.
f = Flecha del arco.
|
Para calcular el espesor en la clave, se tiene la siguiente expresión:
Donde:
tc = Espesor en la clave en metros.
L = Luz del arco en metros.
q = Sobrecarga en Kn/m2
gc = Carga muerta en la clave en Kn/m2
Para el espesor en los arranques es aconsejable tomar espesores comprendidos entre 1.5 a 3 veces el espesor en la clave, siendo frecuente 2* tc .
Para calcular espesores del arco en cualquier sección, se tiene:
Donde:
tx = Espesor perpendicular al eje de una sección cualquiera.
ta = Espesor en el arranque.
fa = Ángulo en el arranque.
f = Ángulo en la sección en estudio.
Estas expresiones permiten predimensionar la estructura para luego entrar a la verificación como ser en el caso de las bóvedas en que las componentes del polígono de las fuerzas no deben salir del tercio central de la sección transversal.
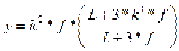
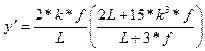
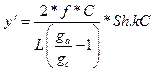
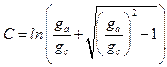
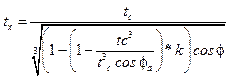
0 comentarios::
Publicar un comentario