Una vez tamizado el árido se grafica en papel semilogarítmico el porcentaje que pasa por cada tamiz vs. las aberturas de los tamices en mm.
FIGURA Grafica de gradaciones del agregado. Gradación de la arena a la izquierda y la del agregado grueso a la derecha.
En general las normas establecen límites entre los cuales se deben encontrar las curvas granulométricas, para considerar al árido como adecuado para el preparar el Hormigón.
En la figura se han trazado las gráficas correspondientes al agregado fino y al grueso de las tablas vistas en la entrada Modulo de Finura, en las que aparecen áreas sombreadas con las que se indican los límites permisibles de gradación para los respectivos agregados, según se especifican en la ASTM C33. Esas gráficas de gradaciones revelan tendencias que son difíciles de estimar a partir de datos tabulados. Por ejemplo, la gráfica revela con claridad que el agregado grueso de la tabla está muy cerca de no cumplir con la establecido para la gradación de 1” a №4 respecto a la cantidad que pasa el tamiz de ⅜”, ya que la curva real de gradación casi queda fuera del área sombreada.
Los espaciamientos horizontales de la figura son proporcionales al logaritmo de la abertura del tamiz.
Otras teorías utilizan curvas teóricas para el árido total (grava mas arena), con una forma parabólica que se aproxima a la gradación de máxima densidad y mínimo contenido de vacíos. Existen varios métodos para obtener curvas adecuadas a cada caso, cada uno de los cuales tiene su propio campo de aplicación. De estos métodos algunos se refieren a granulometrías continuas, en el que se encuentran presentes todos los tamaños de granos y otros a granulometrías discontinuas, en el que faltan algunos elementos intermedios, por lo que la curva granulométrica presenta un escalón horizontal, pudiendo decirse como idea básica que el primero es más trabajable y menos expuesto a segregación que el segundo, aunque con el segundo se pueden conseguir mayores resistencias cuando se estudia y fabrica cuidadosamente.
a) Parábola de Fuller.- Para hormigón armado, con áridos redondeados cuyo tamaño máximo sea de 50 ± 20 mm. y contenido de cemento no inferior a 300 Kg/m3, se obtienen buenos resultados mediante granulometrías continuas que siguen la siguiente ecuación:
Donde:
p = porcentaje en peso que pasa por el tamiz.
d = abertura (diámetro) de cada tamiz.
D = tamaño máximo (diámetro) del árido.
La tabla siguiente muestra los módulos de finura de áridos que siguen la parábola de Fuller según el tamaño máximo de árido.
TABLA MÓDULO DE FINURA DE ÁRIDOS QUE SIGUEN LA PARÁBOLA DE FULLER SEGÚN EL TAMAÑO MÁXIMO DE ÁRIDO.
En hormigón armado, con áridos rodados cuyo tamaño máximo se encuentre entre 30 y 70mm, el empleo de la parábola de Fuller da buenos resultados, siempre que no existan secciones fuertemente armadas. Cuando se emplean áridos de machaqueo o en secciones muy armadas, puede emplearse el mismo método con algunas correcciones finales, en el sentido de aumentar algo el árido fino acosta del grueso.
b) Parábola de Bolomey.- En esta curva granulométrica se considera incluido el cemento, y su campo de aplicación es mucho mas amplio que el de la parábola de Fuller.
Donde:
p = porcentaje en peso que pasa por el tamiz.
d = abertura (diámetro) de cada tamiz.
D = tamaño máximo (diámetro) del árido.
a = según la segunda tabla
TABLA VALORES DE “A” PARA LA PÁRABOLA DE BOLOMEY
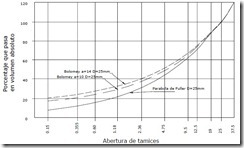
FIGURA Parábola de Fuller y curva de Bolomey
c) Método del Modulo de Finura.- según Abrams, Hummel y otros autores, no es necesario ceñirse exactamente a una curva granulométrica teórica, sino que basta que el modulo de finura del árido sea el mismo que el de la curva teórica adoptada.


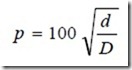
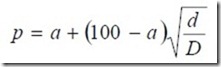

0 comentarios::
Publicar un comentario