Grietas por flexión

Las fisuras por flexión se inicia en la armadura, progresa en vertical hacia la fibra neutra y se encorva al final, buceando el punto de aplicación de la carga y determinándose al alcanzar la cabeza de compresión. Estas fisuras avisan con mucho tiempo.

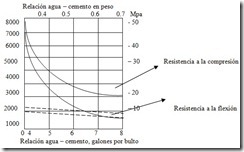
Fig. Efecto de la relación agua – cemento en la resistencia a la compresión y a la tensión por flexión a los 28 días

En cualquier sección trasversal existen fuerzas internas que pueden descomponerse en fuerzas normales y tangenciales, tracción en un lado y compresión en el otro del eje neutro, su función es resistir el momento flector que actúa en la sección.

Los supuestos fundamentales relacionados con la flexión son los siguientes:

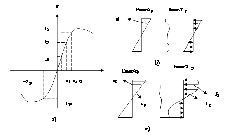
1. El esfuerzo de la flexión f en cualquier punto depende de la deformación unitaria en tensión y en compresión ver figura a, si la deformación unitaria máxima en fibra exterior es menor que la deformación unitaria ε_p, entonces los esfuerzos y las deformaciones son proporcionales figura b.si la deformación máxima unitaria en la fibra exterior es mayor que ε_p lo anterior ya no es valido el resultado es el que se ve en la figura c.

2. La distribución de los esfuerzos cortante v, en la altura de la sección depende de la forma de la sección trasversal y del diagrama ε y f unitario estos esfuerzos cortantes son máximos en el eje neutro o iguales a los esfuerzos cortantes en los planos H y V a través de cualquier punto son iguales.

3. Debido a la acción combinada de estos se presentan los esfuerzos inclinados de tensión y compresión en cualquier punto de la viga de los cuales el mayor forma 90° con el otro, la magnitud del máximo esfuerzo inclinado esta dado por:

Donde:

t = Esfuerzo de tensión diagonal

f = Magnitud del esfuerzo normal

v = Magnitud del esfuerzo cortante

El esfuerzo inclinado forma un Angulo α con la horizontal.

Fig. Distribución de esfuerzos elásticos e inelásticos

4. Cuando los esfuerzos en las fibras exteriores son menores que el limite de proporcionalidad fp, la viga se comporta elásticamente como se ve en la figura b, el esfuerzo en cualquier punto de la sección transversal esta representado por la ecuación.

Donde:

f =Esfuerzo de flexión a una distancia y medida desde el eje neutro

M =Momento flector exterior en la sección

I = Momento de inercia de la sección trasversal con respecto al aje neutro

El escuezo de flexión máximo ocurre en las fibras exteriores y es igual a:

Donde:

c = Distancia desde el eje neutro hasta la fibra exterior

S = I/c Modulo de elasticidad de la sección trasversal

El esfuerzo cortante longitudinal igual a la trasversal v en cualquier punto de la sección transversal esta dado por:

Donde:

V = Cortante total en la sección

Q = Momento elástico con respecto al eje neutro de aquella porción trasversal

b = Ancho de la viga en determinado punto

Comportamiento del hormigón armado

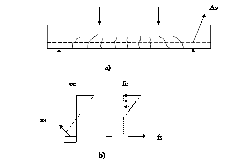
En consecuencia estas fallan en el lado sometido a tensión a cargas mucho mas antes de que se desarrolle la asistencia completa del concreto en el lado de la compresión, cuando la carga en dicha viga se incrementa de forma gradual de modo que producirá la falla ver figura a, en esta etapa se desarrollaran las grietas de tensión. Estas se propagan con la rapidez arriba y muy cerca del nivel del plano neutro.

La distribución de deformaciones unitarias y esfuerzos en la sección fisurada o cerca de ella como se ve en la figura b.

Fig. Comportamiento de concreto reforzado ante carga creciente

Esfuerzos elásticos y sección fisurada o agrietada

Cuando el esfuerzo de tracción fct, exceda al modulo de rotura se forman grietas como aparece en la figura.

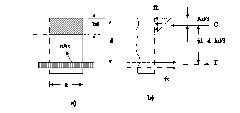
Para calcular los esfuerzos si se desea hacerlo con las deformaciones unitarias puede usarse el artificio de la sección trasformada, solo es necesario tener en cuenta el echo de que todo el concreto sometido a esfuerzos de pensión se supone agrietado ver figura a.La sección transformada consiste que el concreto sometido a compresión en un lado del eje y n veces el área del acero de tensión en el otro. Las fuerzas que actúan en la sección trasversal estas aparecen en la figura b.

Para determinar ubicación el eje neutro el momento de área de tensión con respecto al eje, con el momento del área de compresión lo que da como resultado.