Actúan fuerzas de torsión que tienden a retorcer al elemento con respecto a su eje longitudinal; estas fuerzas de torsión rara vez actúan solas, casi siempre están acompañadas por momentos flectores, por cortantes transversales y algunas veces por fuerzas axiales.
La torsión es un efecto secundario, al considerar los efectos de torsión en las estructuras de concreto reforzado es importante diferenciar entre la torsión primaria y la torsión secundaria.
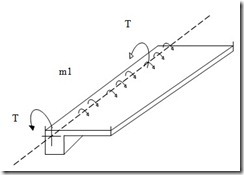
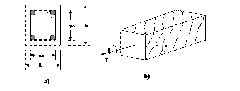
La torsión primaria llamada torsión de equilibrio, se presenta cuando la carga externa no tiene otra alternativa que ser resistida por torsión como se ve en la figura a.se ilustra una losa en voladizo.
Fig. a Torsión Primaria o de equilibrio en la losa de voladizo
En cortante con la condición anterior se genera la torsión secundaria, se debe considerar para esto una continuidad en el diseño, si no se considera esto se presenta el agrietamiento. Esto se da en vigas de borde que sostiene una losa monolítica de concreto como aparece en la figura b.
Fig. b Torsión secundaria o de compatibilidad en una viga de borde
Torsión en elementos de hormigón simple
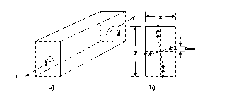
En la figura a se señala una porción de un elemento prismático sometida a momentos torsores T, iguales y opuestos en los extremos, si el material es elástico la teoría de torsión indica que los esfuerzos cortantes por torsión se distribuyen sobre la sección transversal como se muestra en la figura b, los mayores esfuerzos cortantes se presentan en la mitad de la caras mas anchas.
Fig. Esfuerzos causados por la torsión
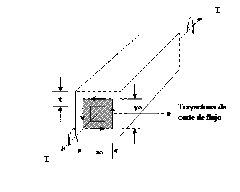
Cuando los esfuerzos de tensión diagonal exceden la resistencia a tensión del concreto, se forman grietas en algún sitio accidentalmente más débil y esta se propaga. El valor del momento torsor que corresponde a la formación de grieta diagonal se conoce como torque de agrietamiento Tcr, tenemos un tubo delgado bajo torsión.
Fig. Tubo de pared delgado bajo torsión
(a)
(b)
(c)
(d)
Donde:
q = Cortante alrededor del perímetro del tubo
yo = Longitud a través de la pared vertical
xo = Longitud a través de la pared horizontal
t = Espesor finito alrededor de la superficie del elemento
Ao = Área encerrada por la trayectoria de fuga de corte
Para un espesor de pared de tubo el esfuerzo cortante unitario que actúa dentro de la pared del tubo.
Donde:
σ = τ = Esfuerzo principal de tensión de manera que el concreto se agrieta solo cuando τ = σ = 
= Es la resistencia de la tensión del concreto.
=Es el perímetro de la sección transversal
y 
Donde:
Ares encerrada por el perímetro externo de la sesión trasversal completa de concreto
Perímetro de la sección trasversal
Se ha encontrado que la ecuación permite estimar de manera razonable el momento torsor de agrietamiento para elementos de concreto reforzado independientemente de la forma de su sección transversal.
Torsión en elementos de hormigón armado
Para resistir la torsión para valores de τ superiores a Tcr el esfuerzo debe estar conformado por estribos poco espaciados o por barras longitudinales, las barras longitudinales pueden contribuir l la resistencia a torsión ver Figura.
Fig. Grietas de torsiones vigas
Tenemos que.
(a)
(b)
Donde:
At = Área de una rama de estribo
Fyv = Resistencia de afluencia al refuerzo transversal
n = Numero de estribos interceptados en la grieta
Fig. Donde a) Tensión vertical de estribos b) Compresión diagonal c) Diagrama de equilibrio al cortante
De modo que.
(c)
Combinando las ecuaciones a y b se tiene.
(d)
Donde:
ΔN =Fuerza de tensión axial
Ph =Perímetro de la línea central de los estribos serrados
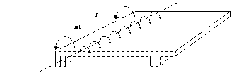
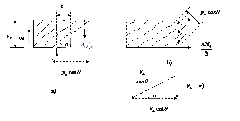
0 comentarios::
Publicar un comentario