FLUJO EN ORIFICIOS, TEOREMA DE TORRICELLI

El termino orificio, según se usa en hidráulica, se aplica a cualquier abertura, con perímetro cerrado, practicada en una pared o tabique que permite el derrame del agua contenida en un recipiente. Los orificios entran en el diseño de muchas estructuras hidráulicas; y se usan frecuentemente en la medición de caudales de las corrientes fluidas.
Los mas usados son lo circulares, El agua que fluye por orificios de conforme va abandonando el orificio, el chorro va contrayéndose gradualmente, hasta formar un chorro cuya área transversal es algo menor que el área transversal del orificio. Esto se debe a la convergencia de las trayectorias seguidas por las diferentes partículas, conforme se acercan al orificio. Supóngase un deposito de liquido, este tiene en la parte inferior un orificio por el que sale el liquido; el área del orificio es pequeño y el de el deposito es suficientemente grande, y siendo el flujo permanente, de manera que el gasto que sale por el orificio es igual al gasto que entrara en el deposito, por lo que se tendrá una altura del liquido “h”.

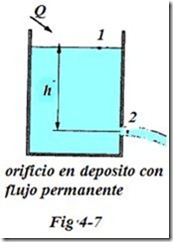
Suponiendo el flujo ideal, podemos partir de la ecuación de Bernoulli entre el punto “0” en la superficie del deposito y el punto de salida del orificio.

Vemos que P₀=P_s; V₀ =es aproximadamente cero y z_s =0, tendremos:

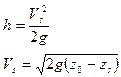
 [m/s]
esta última ecuación se conoce como Teorema de Torricelli.
 
Donde la velocidad es igual a la que adquiriría una partícula de fluido al caer libremente desde una altura “h” (velocidad ideal) y esta es independiente del peso especifico del fluido; con alcohol y mercurio la velocidad seria la misma.
En un orificio situado en un plano horizontal, todas sus partes estarán bajo las mismas cargas, y la velocidad de todas las partículas será igual, al llegar a la sección contraída. en este caso el chorro de agua se elevaría hasta una altura igual a la carga que produce. Por supuesto, que la resistencia del aire impide que esto suceda en la realidad, como también lo impiden la fricción entre el agua y el orificio, y la fricción de las partículas de agua. Los experimentos han enseñado que, para cargas bajas (< 2 y 2.5 metros), la discrepancia es muy pequeña, aumentando conforme aumenta la carga.
Para desarrollar este caso podemos partir de Bernoulli. Primero obtenemos una expresión para la velocidad del chorro en el punto 2.


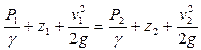
ahora se escribe la ecuación de Bernoulli entre los puntos 2 y 3 en el nivel de la superficie libre del fluido:

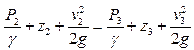
Pero . Entonces para , tendremos:

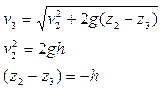
Tenemos:
 [m/s]
este resultado verifica que la corriente alcanza justamente la altura de la superficie libre de fluido en el tanque.
Para alcanzar una altura mayor (fuentes), se puede desarrollar una mayor presión por encima del fluido en el recipiente, o se puede utilizar una bomba para obtener una mayor presión.
Otras consideraciones del flujo de orificios:
TRAYECTORIA DE LA VENA LIQUIDA
COEFICIENTE DE VELOCIDAD
COEFICIENTE DE CONTRACION
COEFICIENTE DE GASTO O DESCARGA
PERDIDA DE CARGA EN UN ORIFICIO
ORIFICIO SUJETO A CARGAS BAJAS
ORIFICIOS SUMERGIDOS O AHOGADOS
ORIFICIO EN LAS TUBERIAS
GASTO EN ORIFICIOS DE PARED GRUESA