En la sección anterior se estudio el uso del principio de Müller-Breslau para dibujar la línea de influencia de la reacción, fuerza cortante y momento en un punto de una viga estáticamente determinada. En esta parte del capitulo extenderemos este método y lo aplicaremos a vigas estáticamente indeterminadas. Hay que recordar que, para una viga, el principio de Müller-Breslau establece que la línea de influencia para una función (reacción, fuerza cortante o momento) es, a la misma escala, la forma deflexionada o línea elástica de la viga cuando sobre ésta actúa la función. Para dibujar la línea elástica apropiadamente, la capacidad de la viga para resistir la función aplicada debe cancelarse de modo que la viga pueda deflexionarse cuando la función se aplique. Para vigas estáticamente determinadas, las formas deflexionadas (o líneas de influencia) serán una serie de segmentos rectos. Sin embargo, para vigas estáticamente indeterminadas, se tendrán líneas curvas. Ahora se podrá observar la construcción de cada uno de estos tres tipos de líneas de influencia (reacción, fuerza cortante y momento) para una viga estáticamente indeterminada. En cada caso ilustraremos la validez del principio de Müller-Breslau usando el teorema de Maxwell sobre los desplazamientos recíprocos.
Reacción en A
Para determinar la línea de influencia para la reacción en A en la figura a, se coloca una carga unitaria sobre la viga en puntos sucesivos y en cada caso se calcula la reacción en A. La gráfica de los resultados representa la línea de influencia. Por ejemplo, cuando la carga está en el punto D, figura a, la reacción en A, que representa la ordenada de la línea de influencia en D, puede calcularse por el método de las fuerzas. Para ello, se aplica el principio de superposición como se muestra en las figuras a a la c. La ecuación de compatibilidad para el punto A es entonces:
0 = fAD + RA fAA o RA = - fAD / fAA
Sin embargo, se sabe por el teorema de Maxwell, sobre los desplazamientos recíprocos, que fAD = - fDA , d, por lo que podemos también calcular RA (u ordenada de la línea de influencia en D) usando la siguiente ecuación:
Por comparación, el principio de Müller-Breslau implica quitar el soporte en A y aplicar en su lugar una carga unitaria vertical. La curva deflexionada resultante, figura 3.22.d, es a cierta escala la forma de la línea de influencia para Ay. Sin embargo, de la ecuación anterior se ve que el factor de escala es (1/ fAA).
Fuerza cortante en E.
Si debe determinarse la línea de influencia para la fuerza cortante en el punto E de la viga en la figura a, entonces por el principio de Müller-Breslau, la viga se imagina cortada en este punto y se inserta en E un rodillo guiado, figura b. Este dispositivo transmitirá un momento y una fuerza normal pero ninguna fuerza cortante. Cuando la viga se deflexiona debido a las cargas cortantes unitarias positivas que actúan en E, la pendiente a cada lado del rodillo se mantiene constante y la curva de deflexión representa a cierta escala la línea de influencia para la fuerza cortante en E , figura c. Si se hubiese aplicado el método básico para establecer la línea de influencia para la fuerza cortante en E , habría sido necesario aplicar una carga unitaria en cada punto D y calcular la fuerza cortante interna en E, figura a. Este valor VE, representaría la ordenada de la línea de influencia en D. Mediante el método de las fuerzas y el teorema de Maxwell sobre los desplazamientos recíprocos, como en el caso anterior, puede demostrarse que
Esto establece de nuevo la validez del principio de Müller-Breslau, esto es, que una carga cortante unitaria positiva aplicada a la viga en E, figura c, ocasionará que la viga se deflexione según la línea de influencia para la fuerza cortante en E. Aquí el factor de escala es (1/fAA).
Momento flexionante en E.
La línea de influencia para el momento flexionante en E en la figura a puede determinarse colocando una articulación en E, ya que esta conexión transmite fuerzas normales y cortantes pero ningún momento, figura b. Mediante un par de momentos unitarios positivos, la viga asumirá la forma deflexionada indicada por la línea segmentada que se muestra en la figura c, que representa a cierta escala la línea de influencia, nuevamente se puede observar una consecuencia del principio de Müller-Breslau.
Con el método de las fuerzas y el teorema de Maxwell, podemos demostrar que:
El factor de escala aquí es (l / aEE).
Procedimiento de análisis.
El siguiente procedimiento proporciona un método para determinar la línea de influencia para la reacción, la fuerza cortante o el momento flexionante en un punto de una viga usando el principio de Müller-Breslau.
Línea de influencia cualitativa En el punto de la viga en que va a determinarse la línea de influencia, coloque un dispositivo que cancele la capacidad de la viga para soportar la función de la línea de influencia. Si la función es una reacción vertical, use un rodillo guiado verticalmente; si la función es la fuerza cortante, use un dispositivo deslizante; o si la función es el momento, use una articulación o pasador. Coloque una carga unitaria en la conexión que actúa sobre la viga en la "dirección positiva" de la función. Dibuje la curva elástica para la viga. Esta curva representa a cierta escala la forma de la línea de influencia para la viga.
Línea de influencia cuantitativa Si van a determinarse valores numéricos de la línea de influencia, calcule el desplazamiento de puntos sucesivos a lo largo de la viga cuando ésta, está sometida a la carga unitaria colocada en la conexión mencionada arriba. En general, es aconsejable usar el método de la viga conjugada para los cálculos. Divida cada valor del desplazamiento por el desplazamiento determinado en el punto en que actúa la carga unitaria. Aplicando este factor de escala, los valores resultantes son las ordenadas de la línea de influencia.





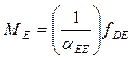

0 comentarios::
Publicar un comentario