Las siguientes clases de puentes con cantiliver serán discutidos:
a) Puentes de un tramo central con dos cantiliver en voladizo.
b) Puentes cantiliver con contrapeso.
c) Puentes de varios tramos provistos cada uno de ellos de uno o dos cantilivers.
Momento resistente, fuerza cortante en una viga de un paño con dos cantilivers.
Una viga de un tramo con dos cantilivers es estáticamente determinado.
Las fuerzas situadas sobre el cantiliver producen un momento resistente y fuerza cortante no solamente en el cantiliver sino también en el paño central de la viga. En cambio las fuerzas continuadas en el tramo central no tiene efecto en el cantiliver.
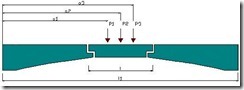
| Notación: | ll | Longitud del cantiliver. |
| l | Longitud de la viga en el tramo central. | |
| P1, P2, P3 | Fuerzas concentradas sobre el cantiliver | |
| a1, a2, a3 | Distancias el apoyo a las fuerzas P1,P2. | |
| Mc | Momento resistente en el apoyo debido a las fuerzas sobre el cantiliver. | |
| Vc | Fuerza cortante en el apoyo, debido a las fuerzas en el cantiliver. | |
| Mcx | Momento resistente en el cantiliver en un punto situado a una distancia x del apoyo. | |
| Vx | Fuerza cortante en el cantiliver en un punto x del cantiliver |
Cantiliver.
Fórmulas para cantilivers cargados uniformemente ó por fuerzas concentradas, las fórmulas para fuerzas cortantes y para momentos resistentes en los cantiliver son las siguientes:
| FUERZAS UNIFORMEMENTE DISTRIBUIDAS | FUERZAS CONCENTRADAS | ||
| ESFUERZOS CORTANTES | Vc en apoyo Vcx en un punto x | WL1 W(L1-x) | P1+P2+P3 P1+P2 |
| MOMENTOS RESISTENTES | Mcx en apoyo Mcx en un punto x | ½(WL12) -1/2W(L1-x)2 | -(P1a1+P2a2+P3a3) -P1(a1-x)+P2(a2-x) |
Viga principal en el tramo central.
Momentos resistentes y esfuerzos cortantes en el tramo central debido a fuerzas sobre el cantiliver, son los siguientes:
Esfuerzos cortantes: (constantes a través del tramo).
Considerando fuerzas del cantiliver izquierdo:
Vx = -Mc1/l (1)
Considerando fuerzas del cantiliver derecho:
Vx = Mc2/l (2)
Considerando las fuerzas de ambos cantiliver:
Vx = (-Mc1-Mc2)/l (3)
Vx = 0 cuando Mc1= Mc2 (4)
Momentos resistentes.
Para un lado cargado, el momento resistente negativo varia da acuerdo a una línea recta, con el máximo sobre el apoyo siguiente al tramo cargado del cantiliver y acero en el apoyo.
Cuando ambos cantilivers son cargados, los momentos restantes en el paño varían de acuerdo a una línea recta, del momento resistente del cantiliver Mc1 en un apoyo al momento resistente del cantiliver Mc2 en otro apoyo. Cuando Mc1, Mc2, el momento resistente en el tramo central es constante ó igual a Mc1.
Posición más desfavorable de fuerzas vivas sobre el cantiliver
La posición mas desfavorable de fuerzas vivas uniformemente distribuidos (sobrecarga) ó cuando el cantiliver esta enteramente cargado. La más desfavorable posición de fuerzas concentradas es cuando la fuerza está situada en el punto final del cantiliver
Momentos resistentes y esfuerzos cortantes para pesos muertos en vigas con cantiliver.
Para cargas muertas, ambos cantiliver y el tramo principal será considerado como cargado simultáneamente. EI diagrama de momentos resistentes para cargas muertas es dado en la figura 6.5. En los apoyos los momentos resistentes son iguales al máximo momento negativo de los cantilivers Mcl y Mc2 respectivamente. Considerando la línea del diagrama de momentos se cuelga una parábola determinada por los momentos resistentes debidos a los cargas sobre el tramo, con lo que se completa el diagrama de momentos.
Los esfuerzos cortantes en el paño principal son iguales esfuerzos cortantes debido a las fuerzas sobre el paño principal y a las fuerzas sobre él cantiliver, computadas de la fórmula (1). Para cantilivers simétricamente cargados este esfuerzo cortante es igual a cero.
Momento resistente y esfuerzo cortante para fuerzas vivas.
Para un tren de carga, el momento resistente positivo en el tramo principal es el mismo que para un simplemente apoyado. El momento negativo máximo debido a las fuerzas del cantiliver puede no ser considerado como que esta reduciendo el momento positivo en el paño principal porque el paño principal puede estar enteramente cargado cuando no hay fuerzas sobre el cantiliver.
El mayor momento negativo para fuerzas vivas en el tramo principal es producido cuando ambos cantilivers son enteramente cargados y no hay fuerzas sobre este tramo.
El máximo esfuerzo cortante en el tramo principal es producido cuando se suma él producido por la más desfavorable posición sobre el tramo principal, el que resulta de cargar uno de los cantiliver.
Para el esfuerzo cortante positivo, el cantiliver izquierdo es cargado.
Envolvente de momentos resistentes para fuerzas vivas y muertas.
En envolvente de momentos, incluyendo impacto, cuando ambos valores son del mismo signo se suman y cuando ambos valores son de diferente signo se restan. Cuando el momento resistente de fuerzas muertas es de signo diferente al de fuerzas vivas, es mejor dividir por un factor de seguridad usualmente 2 siendo antes substraído del momento resistente para fuerzas vivas.
La envolvente de momentos se usará para determinar las dimensiones de la viga en los diferentes puntos, el número y la longitud de barras de refuerzo y los puntos de inflexión.
Momentos resistentes y esfuerzos cortantes en un tramo central con un voladizo como cantiliver
Para una viga con un cantiliver los momentos resistentes y los esfuerzos cortantes pueden ser hallados usando las formulas (1) y (4). Los diagramas de momentos resistentes y de esfuerzos cortantes son determinados de la misma manera que para vigas de dos cantiliver, excepto que el momento resistente en el extremo en que no hay cantiliver es cero.
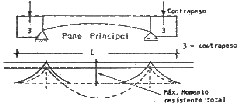
Puentes de contrapeso.
El propósito de estos puentes es producir en los apoyos momentos negativos muy grandes reduciendo el momento positivo en el centro del paño principal.
Un primer paso en el diseño de la estructura, es el diseño de la losa del tramo central. Es una desventaja adoptar
Una losa ligera porgue al reducir el peso muerto del paño o tramo principal el peso requerido para el contrapeso también es reducido. Un concreto de agregados finos puede ser económico, un arreglo consistente en losas de paneles soportadas sobre cuatro lados y armada en dos direcciones, también puede ser hallada económica.
Luego tantear las alturas de las vigas en el centro y en los apoyos. El acartelamiento de la viga puede ser parabólica o segmental o puede tener la porción central recta y provista en los extremos de pequeños acartelamientos. Antes las dimensiones son escogidas, halladas por el máximo momento positivo en el centro del tramo, teniendo en cuenta las fuerzas vivas y las fuerzas muertas, considerándola como una viga simplemente apoyada. Como lo indica el diagrama.
Usando la altura asumida de la viga como una guía, decidimos la distribución del momento total máximo de la viga entre el momento positivo y negativo. El momento negativo aceptado, este determina la longitud y peso del cantiliver. Para completar el diagrama de momentos para el tramo central, el momento resistente debido a las fuerzas vivas sobre el cantiliver serán adicionadas, como lo demuestra la figura anterior.
El contrapeso decidido por el momento máximo del cantiliver para fuerzas muertas, algunas combinaciones pueden ser ensayadas. Es posible usar pequeños cantiliver con pesos grandes o viceversa. Pero la longitud de los cantilivers está limitada por las relaciones de los cantilivers con el tramo central, relación que varia de 0.2 a 0.35
Puentes de varios tramos provistos de Cantilivers libres.
Su objeto es reducir la altura dé las vigas en el centro del tramo, reduciendo también el costo de las vigas; sin necesidad de recurrir al diseño estáticamente indeterminado.
En comparación con las vigas simplemente apoyadas tienen la ventaja de requerir menor altura de la viga principal en el centro del tramo y menor cantidad de materiales. Las desventajas de estos puentes es la deflexión que sufren los cantiliver al paso de los vehículos. Algunas experiencias ventajosas pueden ser ensayadas para preservar los puntos de unión de los cantiliver, pero la debilidad de todos ellos reside en que entre ambos no trabajan, ó si trabajan las fuerzas al ser transmitidas de uno a otro cantiliver, cambian completamente las condiciones previstas para los esfuerzos de las vigas. El diseño estático determinado se convierte en un diseño indefinido de indeterminación estática.
Puentes Cantilivers con tramos suspendidos.
El objeto del diseño de estos puentes es llegar a adquirir las, ventajas del diseño de vigas continuas, sin las ventajas del diseño estáticamente indeterminado.
Es un hecho conocido que para una condición particular de carga una viga continua puede ser cambiadas por varios tramos estáticamente determinados provistas las luces alternadas de pestañas de enlaces, en los puntos de contra flexión (inflexión) ó sea en los .punios de momentos nulos, la estructura resultante consiste en un número de vigas cantiliver y de pequeñas vigas suspendidas de los cantiliver.
El momento resistente de tal estructura para la carga particular es idéntica con la producida en una viga continua, en una viga que soporta un tren de carga la localización de los puntos de inflexión varia con las condiciones de carga. Existen dos clases de puentes:
a) Puentes simétricos que tienen un número impar de tramos y que pueden tener los tramos extremos suspendidos o anclados.
b) Asimétricos que tienen un número par de tramos.
Ventajas y desventajas de estos puentes.
1.- Requiere menos concreto y acero que las vigas simplemente apoyadas pero más que las continuas.
2.- Requiere menos encofrados que las vigas continuas ya que se puede armar tramo a tramo igual que si fuera simplemente apoyada, no asi el continuo.
3.- En cada pilar el diseño del cantiliver usa tan solo un apoyo requiriendo un menor ancho que la simplemente apoyada que requiere de dos apoyos, con el consiguiente ahorro del material.
4.- La reacción del pilar es siempre centrada; y los apoyos móviles se trasladan a los puntos de menor reacción.
5.- Su principal ventaja sobre el continuo es que soporta asentamientos en los apoyos sin que ocasione esfuerzos en la estructura.
Como desventajas en comparación con las simplemente apoyadas, es que el diseño del cantiliver requiere algo mas de pericia de parte del diseñador y el arreglo des los esfuerzos es algo más complicado.
En comparación con las vigas continuas el diseño del cantiliver tiene la ventaja de que son estáticamente determinadas y que la posibilidad de malos efectos por un desigual asentamiento de los apoyos es menor. Siendo la desventaja que el costo de estos puentes es algo mayor debido al costo extra de las pestañas de enlace y de las uniones entre los tramos suspendidos con los extremos de los cantilivers, y finalmente que el diseño del cantiliver es menos rígido quo el continuo.
Diseño de cantiliver con tramos suspendidos.
EI tablero incluyendo lasas, sardineles, barandas se hacen en igual forma que en los casos anteriores. Existen tres clases de vigas principales:
1°) En tramo de anclaje con voladizo.
2°) Tramo suspendido que va entre las juntas de voladizo o entre el voladizo y el estribo.
3º) Tramo intermedio que aparece en los puentes de más de tres tramos, es un tramo con dos voladizos.
| El dimensionamiento de las vigas principales tiene por objeto igualar los momentos en los apoyos, igualar las luces de los tramos intermedios, no así en los extremos que tienen una luz que es los 2/4 de la luz del tramo intermedio, el tramo suspendido la mitad de la luz del tramo intermedio. Las relaciones recomendables entre las alturas en el centro del tramo y el apoyo son: Para puentes losas o para vigas huecas: Para puentes de tablero superior o viga T |
Como los momentos de inercia en esta clase de viga es variable, equivale gastar más encofrado, por eso en puentes pequeños no vale la pena hacerlo de altura variable; las luces mas económicas son:
Para puentes losas hasta 15 m.
Para puentes de tablero superior ó viga T de 15 a 25 m.
De 25 a 35 m. viga hueca en zona de momento negativos y viga T en zonas de momentos positivos.
Para puentes de luces mayores de 35 m; se hace totalmente de vigas huecas, que vienen a ser vigas T que presentan dos ventajas:
a) Losa en compresión.
b) Da lugar a la expansión del fierro.
La losa puede tener tres formas de colocación:
a) Corrida a lo largo del puente; se la necesita por compresiones en los apoyos y en los otros sitios por expansión, generalmente usadas en luces mayores de 30 metros. Tiene la ventaja de la buena distribución, pero la desventaja es que no se puede recuperar el encofrado; para recuperarlo habría la necesidad una serie de huecos, otra dificultad es la relativa a las viguetas.
b) Losa común en la zona de compresión. Aquí la recuperación del encofrado puede hacerse, pero no cumplir la ventaja de ensanchamiento
c) Colocar la losa en la zona de momentos negativos pero de sección variable, disminuyendo la sección conforme disminuye los docentes negativos.
Determinación de los momentos resistentes y esfuerzos cortantes
Vigas suspendidas por cantilivers
No es necesario considerarlo aquí ya que su diseño es el mismo que cuando se ha tratado de vigas de puentes losas, exceptuando las vigas en los extremos en los cuales se colocan unas pestañas de enlace que trataremos más adelante.
Vigas con cantiliver
Los momentos resistentes en las vigas con cantilivers son hallados separadamente para las fuerzas sobre el caníiliver y para aquellas sobre el mismo tramo los resultados son combinados.
Momentos resistentes con cantilivers
El momento resistente en cantiliver para vigas con uno o dos cantilivers, puede ser hallado por medio de las siguientes reglas:
Para fuerzas muertas y sobrecarga, el máximo momento es obtenido considerando el tramo suspendido por los cantilivers como enteramente cargado. EI cantiliver está entonces sujeto a fuerzas concentradas actuando en los extremos del cantiliver, que son iguales a las reacciones del tramo suspendido por la acción de las fuerzas muertas. Los momentos resistentes son hallados entonces por la fórmula para cantilivers.
Para un tren de cargas la posición más desfavorable ocurre cuando está situada en el extremo del cantiliver y el tramo suspendido en el cantiliver es cargado por todas las fuerzas del tren de carga qué pueden ser acomodadas en él.
Momento resistente del tramo principal
Para cargas muertas todos los momentos positivos sobre el tramo principal pueden ser consideradas como reducidos por el momentoo resistente del cantiliver en los apoyos de igual manera como los hallados cuando se trató de vigas con uno o más cantilivers.
Para fuerzas vivas los momentos positivos si se tratase de vigas simplemente apoyadas. Los momentos negativos en el tramo principal son producidos, cuando los cantilivers están enteramente cargados y el tramo descargado.
Esfuerzos cortantes
Para fuerzas muertas y sobrecargas, los esfuerzos cortantes exteriores en los cantilivers varían de un mínimo en .el extremo donde es igual a la reacción del tramo suspendido, a un máximo en el apoyo donde es igual a la reacción del tramo suspendido más todos los pesos sobre el cantilivers.
En el tramo principal, de una viga con dos cantilivers simétricamente cargados, la fuerza cortante para fuerzas muertas es la misma que para una viga simplemente apoyada. Para una viga con un cantiliver la fuerza cortante debida a fuerzas muertas, en el entrante al cantiliver es incrementado por:
Donde Mc(d) es el momento resistente del cantiliver en el apoyo para fuerzas muertas “l” la longitud del tramo. En el extremo libre, el esfuerzo cortante disminuye en el mismo aumento.
Para fuerzas vivas, el esfuerzo cortante en el paño principal es considerado igual al esfuerzo cortante en una viga simplemente apoyada más Mc(l)/l, donde Mc(l) es el momento resistente producido por las fuerzas vivas en el cantiliver siguiente a la mitad del paño considerado. En una viga con un cantiliver no hay incremento en el esfuerzo cortante debido a .las fuerzas vivas en la mitad de la viga siguiente al final libre.
Calculo del extremo del voladizo
El apoyo del tramo suspendido en el cantiliver se hace reduciendo el peralte a la mitad, poniendo lo que se llama una pestaña de enlace. Para reforzar la zona se acostumbra colocar una vigueta transversal entre la parte comprendida entre el tramo extremo y el suspendido.
Se calcula como un cantiliver corriente, siendo el momento igual a la reacción máxima, por la distancia del centro del apoyo a la cara:
Con este momento se calcula al área de acero, recomendándose aumentar ésta área al doble de la que arroje él cálculo, esto como medida de seguridad, teniendo en cuenta que el costo es pequeño con relación al costo del puente.
En el caso de que el área de acero de la loza que se lleva, no es suficiente, se colocarán bastones como lo muestra la figura, en la longitud AB.
Se determinará el esfuerzo cortante que permite calcular los estribos que se recomienda que sean en forma de W y se colocan hasta una distancia igual a la altura del voladizo para evitar rajaduras a 45º.
Esto podrá entenderse mejor con la ayuda del figura:
| |





0 comentarios::
Publicar un comentario