Sin importar su naturaleza, todas las situaciones de flujo están sujetas a las siguientes relaciones, pueden expresarse en forma analítica:
1.- Las leyes de movimiento de Newton, deben cumplirse para cualquier partícula.
2.- La relación de continuidad, es decir, la ley de conservación de la masa.
3.- La conservación de la masa aplicada a mezclas de componentes dentro del fluido.
4.- La primera y segunda leyes de la termodinámica.
5.- Las condiciones de frontera: declaraciones analíticas como por ejemplo que un fluido real tiene velocidad cero con respecto a una frontera en la frontera que los fluidos sin fricción no pueden penetrar una frontera.
También pueden entrar otras relaciones y ecuaciones, tales como una ecuación de estado o la ley de viscosidad de Newton.
En la deducción que sigue el concepto de Volumen de control se relaciona con el sistema en términos de una propiedad general del sistema. En las secciones subsiguientes se aplica específicamente para obtener las relaciones de continuidad, energía y momentum lineal.
Para establecer la relación entre las ecuaciones que se aplican en un sistema y aquellas que se aplican a un volumen de control, considere algunas situaciones generales de flujo en las cuales la velocidad de un flujo, en las cuales la velocidad de un fluido esta dada con respecto a un sistema coordenado xyz. En el tiempo “t” considérese una cierta masa de fluido contenida dentro de un sistema, en el cual tiene las fronteras de líneas puntuadas indicadas. También considérese un volumen de control, fijo con relación a los ejes xyz, que coincide exactamente con el sistema en el tiempo t. En el sistema se ha movido un poco, debido a que cada partícula de masa se mueve a una velocidad asociada con su posición.
Sea N la cantidad total de alguna propiedad (por ejemplo, masa, energía o momentum) dentro del sistema en el tiempo t y sea la cantidad de esta propiedad, por unidad de masa, a través del fluido. La tasa temporal de incremento de N para el sistema se formula ahora en términos del volumen de control.
En (Fig b) el sistema comprende los volúmenes II y III mientras que en el tiempo t este ocupa el volumen II (Fig a).
El incremento en la propiedad N en el sistema en el tiempo esta dado por:
En donde es el momento del volumen. Reordenado, después de sumar y restar
En la derecha y luego dividiendo todo por se llega a:
El término a la izquierda es la tasa temporal promedio de incremento de N dentro del sistema durante el tiempo . En el límite, a medida que
se aproxima a cero, éste se convierte en dN/dt.
Si se toma el limite a medida que se aproxima a cero en el primer termino del lado derecho de la ecuación, las primeras dos integrales son la cantidad de N dentro del volumen de control en
y la tercera integral es la cantidad de N en el volumen de control en el tiempo t. El límite es:
Donde se han utilizado derivadas parciales debido a que el tamaño del volumen de control se mantiene constante a medida que .
El siguiente termino es la tasa temporal del flujo de N hacia fuera del volumen de control, en el limite y puede escribirse como
Donde dA es el vector que representa un elemento de área del área de salida de flujo.
Éste tiene una dirección perpendicular al elemento de área superficial del volumen de control, siendo positivo hacia fuera, y α es el ángulo entre el vector velocidad y el vector de área elemental.
Similarmente, el último término de la ecuación, el cual es la tasa de flujo de N hacia adentro del volumen de control, es, en el límite, igual a:
El signo negativo es necesario debido a que v*dA( ó cos α) es negativo para el flujo de entrada (Fig3-8). Los dos últimos términos de la primera ecuación, dados por las ecuaciones siguientes, pueden combinarse en un termino único que es una integral sobre toda la superficie del volumen de control (sc).
En donde no exista flujo de entrada o de salida v*dA=0; por consiguiente la ecuación puede evaluarse sobre toda la superficie de control. Reuniendo y reorganizando los términos tenemos:
Esta ecuación anterior establece que la tasa temporal de incremento de N dentro de un sistema es exactamente igual a la tasa temporal de incremento de la propiedad N dentro del volumen de control más la tasa neta de flujo de N a través de la frontera del volumen de control.
Esta ecuación se usa para convertir de la forma de sistema a la forma de volumen de control. La forma de sistema, la cual en efecto sigue el movimiento de los paquetes, se conoce como el método Lagrangiano de análisis; la aproximación de volumen de control de conoce como el método Euleriano de análisis, ya que se observa desde un sistema de referencia fijo relativo al volumen de control. Esta ecuación es valida si el volumen de control, fijo en tamaño y forma, tiene una velocidad de traslación uniforme.



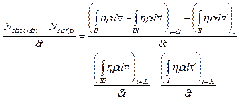


0 comentarios::
Publicar un comentario