La forma de sistema de la conservación de la masa es:
La cual establece que la masa (m), dentro del sistema permanece constante en el tiempo. En la ecuación sea N=m, entonces η es la masa por unidad de masa de η=1, por lo tanto
La ecuación de conservación de la masa establece que la tasa temporal de cambio de la masa en el volumen de control, más la tasa neta a la cual la masa sale del volumen de control a través de su superficie es igual a cero.
Para el desarrollo del subtitulo considérese un tubo cilíndrico. El flujo entra al tubo en la sección 1 y sale en la sección 2.
No se permite flujo a través de la superficie sólida que describe el tubo. La aplicación de la conservación de la masa prosigue de la siguiente manera:
- El volumen de control se define de tal manera que incluya todo el fluido en el tubo dentro de la pared sólida y desde la sección 1 a la 2. Si es posible, todas las secciones de entrada y salida deben definirse o localizarse en regiones donde las líneas de corriente (o tubos) sean paralelas a la frontera, de tal manera que las velocidades de entrada y salida sean perpendiculares a las respectivas áreas.
- Si el enunciado del problema lo permite, es mejor suponer flujo permanente, en cuyo caso la ecuación se reducirá.
- Esta ecuación debe aplicarse a cada superficie de control(sc) donde la masa de fluido, esta entrando o saliendo; entonces tenemos:
- Si los vectores de velocidad a la entra y a la salida son, en cada entrada y salida, perpendiculares a sus respectivas áreas, entonces en las salidas las integrales se evalúan como
y las entradas se evalúan como
. Tenemos:
Nótese que ρ y v todavía son funciones de A1 y A2 y pueden variar dentro de sus respectivas áreas, esto mas que todo en las velocidades.
- Si ρ1 y ρ2 no varían en las secciones transversales de entrada y salida, además conviene evitar velocidades que varíen. Por tanto tomamos la velocidad promedio espacial para reducir el problema a una representación unidimensional.
|
Donde m es la tasa de flujo de masa en Kg/seg. Para el problema de flujo permanente planteado aquí, la ecuación de continuidad dice que la tasa de flujo de masa es constante.
Si el caudal Q (también conocido como tasa de flujo volumétrico o descarga) se define como Q=AV, la ecuación puede tomar la forma de:
Para flujo incompresible permanente, se presenta como forma útil la ecuación siguiente
Para flujo con densidad constante, permanente o no permanente, podemos obtener las ecuaciones para determinar la velocidad, la cual establece que el flujo de volumen neto es cero. Esto implica que el volumen de control está lleno de líquido en todo momento.
EJEMPLO DE APLICACIÓN Por una tubería de 30 cm de diámetro circulan 1800 lt/min, reduciéndose después el diámetro de la tubería a 15 cm. Calcular las velocidades medias en ambas tuberías.
Si existen múltiples entradas y salidas, la ecuación de volumen de control puede extenderse. Supóngase una intersección T; se denotan las condiciones en las entradas (secciones 1 y 3) y en la salida (sección 2). Adicionalmente, suponga que la densidad en cada sección es constante (aunque no necesariamente igual); que los vectores de velocidad son perpendiculares a sus respectivas áreas; y que las velocidades promedios en las secciones transversales, en cada sección, están definidas.


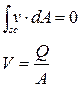
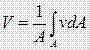




0 comentarios::
Publicar un comentario