En la figura se ilustra un orificio circular de arista viva dentro de un tubo. La velocidad en la vena contracta “2”, se obtiene por la formula,
reemplazando el término de pérdida de energía, h1, por Cv , esta ecuación se transforma en:
En los orificios de los tubos no puede omitirse el factor de corrección por velocidad de acceso (). Nuevamente, haciendo
y
, la expresión para el derrame o gasto se transforma en,
En esta forma la ecuación requiere una solución por aproximaciones sucesivas. Sin embargo, sustituyendo por su valor obtenido de la ecuación de continuidad
, donde A1, es el área del tubo, se deduce la siguiente expresión:
El valor de C varia no solamente con los factores que afectan a los orificios de los depósitos, sino también con la relación del diámetro del orificio, d, al del tubo, d1, y con el lugar donde se efectúan las tomas de presión. Los experimentos indican que la vena contracta esta aproximadamente a la mitad del diámetro del tubo, aguas abajo del orificio. Cuando el orificio esta en el extremo del tubo, p2 es igual a cero en la formula y solamente se requiere un injerto o toma de presión. En la figura se muestran dos curvas que ilustran la relación entre C y el número de Reynolds. Algunas partes de la curva aparecen de trazos porque los valores de R son inciertos, debido a los escasos datos de que se dispone en esta región. En los anexos del presente capitulo se presenta información adicional relativa a los coeficientes de gato o derrame para las tomas de presión en la vena contracta y para los injertos de brida.



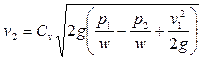



0 comentarios::
Publicar un comentario