TEOREMA DE BERNOULLI - ECUACIÓN DE BERNOULLI

Daniel Bernoulli, en 1738, demostró un teorema general, referente al movimiento de los fluidos, que es probablemente el más importante de la hidráulica. Toda la Hidrodinámica reposa prácticamente en dicho teorema; y gran número de problemas hidráulicos pueden ser resueltos con la única ayuda de dicho teorema. Al enunciarlo y demostrarlo, será mas simple despreciar, al principio, todas las resistencias de fricción e investigar después de la influencia de estas resistencias en los resultados.

De acuerdo con el teorema de Bernoulli, la carga absoluta en cualquier sección transversal es igual a la carga absoluta en una sección de aguas abajo más las perdidas de cargas intermedias. La carga de energía en todas las secciones es constante para corriente uniforme y variable para corriente no uniforme.

Estrictamente hablando, el teorema de Bernoulli solo puede aplicarse a la sección transversal de una corriente cuando la dirección transversal cuando la dirección de ésta sea horizontal. Su deducción se basa en la hipótesis de que todas las velocidades son iguales y que cada punto de la sección tiene el mismo contenido de energía.

Para efectos de demostración, vamos a considerar un flujo ideal, irrotacional, permanente y unidimensional; en el que, analizaremos una línea de corriente, que coincida con el eje de un filete o tubo de corriente, en la que consideramos un elemento diferencial de fluido.

En la vena liquida considerada, ésta tiene un elemento diferencial de área ´dA´ y un elemento longitudinal diferencial ´ds´, por lo que el peso de ella será γdAds. La fuerza que produce la presión en la base inferior del filete será PdA y en el incremento ds la fuerza que produce la presión en la base superior del filete será:

Entonces se puede hacer la sumatoria de fuerzas a través del eje ‘s’ considerado, y aplicamos la segunda ley de Newton:

La aceleración se puede expresar como:

De lo que se obtiene finalmente:

Reemplazando esta ecuación de la aceleración y el coseno equivalente tendremos:

Dividiendo entre el peso específico del fluido y ordenando:

Ecuación de Bernoulli

La ecuación obtenida es la ecuación de Bernoulli; la constante de integración (conocida como constante de Bernoulli) generalmente varía de una línea de corriente a otra, pero permanece constante a lo largo de una línea de corriente en flujo permanente, sin fricción e incompresible. Estas cuatro suposiciones con necesarias y se deben tener presentes al aplicar este ecuación. Cada término tiene dimensiones de (L/T2) o unidades de metros-newtons por kilogramo.

Debido a que 1N=1Kg*m/s2, por consiguiente la Ec-1 se interpreta como energía por unidad de masa.

Puede interpretarse como energía por unidad de peso, metros-newtons por newton. Esta forma es particularmente conveniente para desarrollar problemas de líquidos con una superficie libre.

Cada uno de los términos de la ecuación de Bernoulli puede interpretarse como una forma de energía disponible.

Esta ecuación también se conoce como la ecuación de conservación de energía mecánica. Es particularmente importante notar que esta ecuación de energía se dedujo de la ecuación de momentum.

Las perdidas de energía debida a la fricción y a la transferencia de calor solamente pueden incorporarse a la ecuación diferencial de energía completa.

Al aplicar la ecuación a dos puntos sobre una línea de corriente se obtiene,

Ecuación de Bernoulli desarrollada

Esta ecuación muestra que lo importante es la diferencia en energía potencial, energía de flujo y energía cinética. Por consiguiente, z1-z2 es independiente del nivel de referencia particular, al igual que la diferencia en la elevación de los dos puntos. Similar mente, p1/γ y –p2/γ es la diferencia en las cabezas de presión, expresada en unidades de longitud del fluido fluyendo, y no se altera por la presión de referencia particular seleccionada. Debido a que los términos de velocidad son no lineales, su nivel de referencia es fijo.

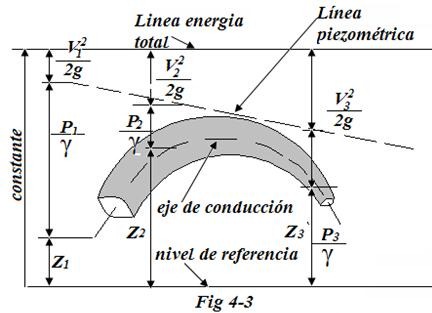
Por tanto los términos de la ecuación de Bernoulli se conocen, a menudo, como cabezas refiriéndose a una altura por encima de un nivel de referencia. El termino Z se le llama cabeza de elevación, y el termino v^2/2g se le conoce como cabeza de velocidad. La suma de las tres se la conoce como cabeza total. Debido a que cada término representa una altura, un diagrama como se presenta en la figura, la cual es la utilidad para visualizar la relación entre los tres tipos de energía. Se observa que, debido a la suposición de que no se pierde o se agrega energía, la cabeza total permanece a un nivel constante. Entonces, la altura relativa de cada término de cabeza varía según lo establecido por la ecuación de Bernoulli.

Como se muestra en la figura, la cabeza de velocidad en la sección 2 será menor que en la sección 1. Esto se puede mostrar mediante la ecuación de continuidad.

Puesto que A1
En resumen, la ecuación de Bernoulli explica el cambio en las cabezas de elevación, de presión y de velocidad entre dos puntos en un sistema de flujo de fluido. Se supone que no existen pérdidas o ganancias de energía entre los dos puntos, de modo que la cabeza total permanece constante. Es esencial que la presión en los dos puntos de referencia se expresen, ambas como presiones absolutas o como presiones manométricas. Es decir, deben tener las dos la misma presión de referencia.